Solutions
Solutions to Try Its
1. Vertices: ; Foci: 2. 3. 4. vertices: ; co-vertices: ; foci: ; asymptotes: ;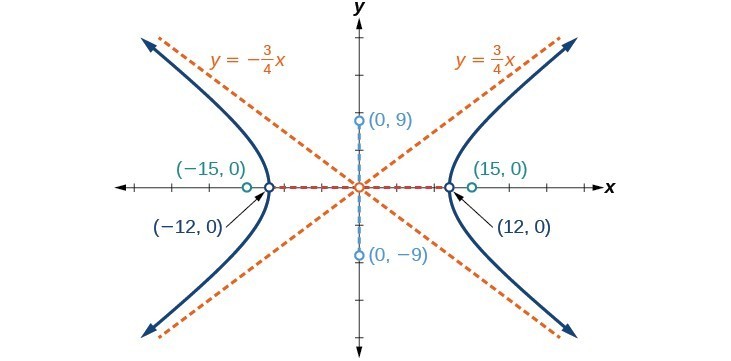 5. center: ; vertices: and ; co-vertices: ; and ; foci: and ; asymptotes:
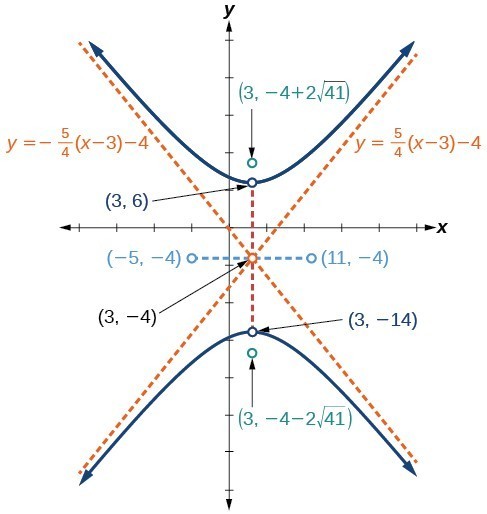
5. center: ; vertices: and ; co-vertices: ; and ; foci: and ; asymptotes:
 6. The sides of the tower can be modeled by the hyperbolic equation. .
6. The sides of the tower can be modeled by the hyperbolic equation. .
Solutions to Odd-Numbered Exercises
1. A hyperbola is the set of points in a plane the difference of whose distances from two fixed points (foci) is a positive constant. 3. The foci must lie on the transverse axis and be in the interior of the hyperbola. 5. The center must be the midpoint of the line segment joining the foci. 7. yes 9. yes 11. ; vertices: ; foci: ; asymptotes: 13. ; vertices: ; foci: ; asymptotes: 15. ; vertices: ; foci: ; asymptotes: 17. ; vertices: ; foci: ; asymptotes: 19. ; vertices: ; foci: ; asymptotes: 21. ; vertices: ; foci: ; asymptotes: 23. ; vertices: ; foci: ; asymptotes: 25. ; vertices: ; foci: ; asymptotes: 27. 29. 31.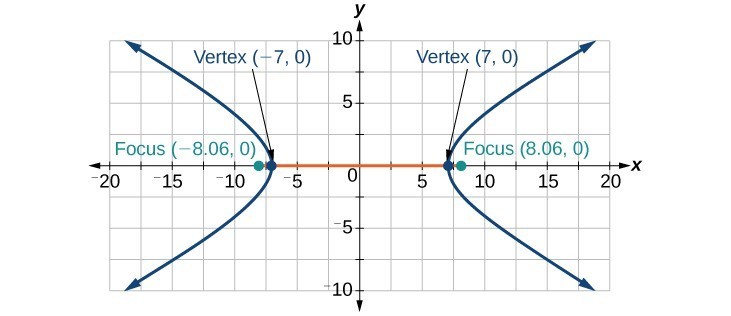 33.
33.
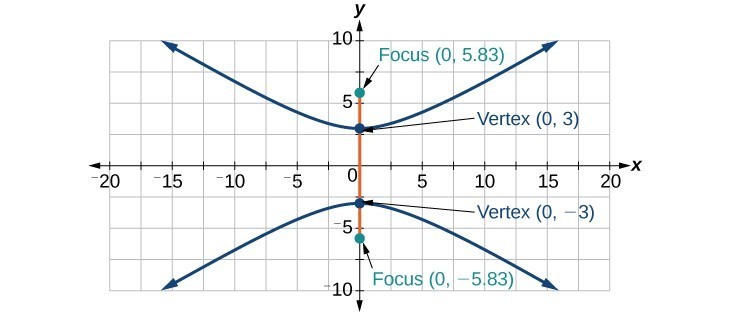 35.
35.
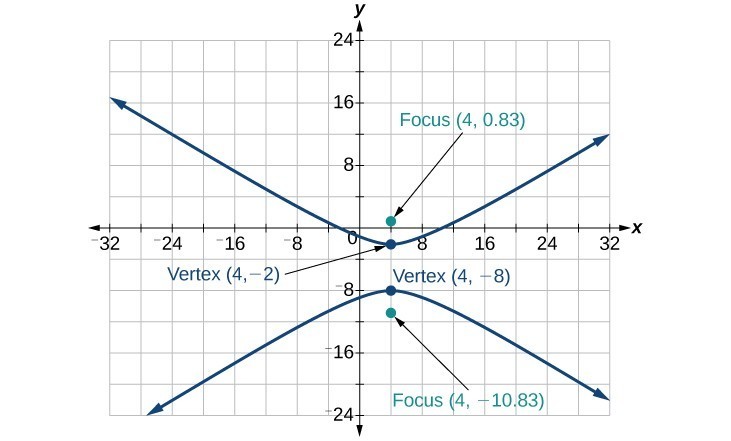 37.
37.
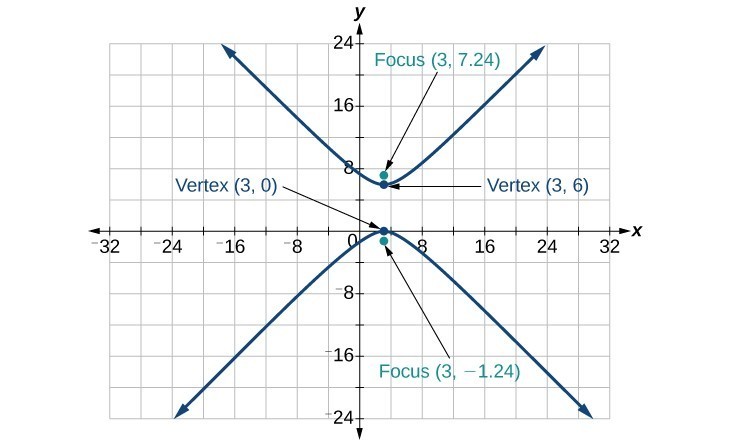 39.
39.
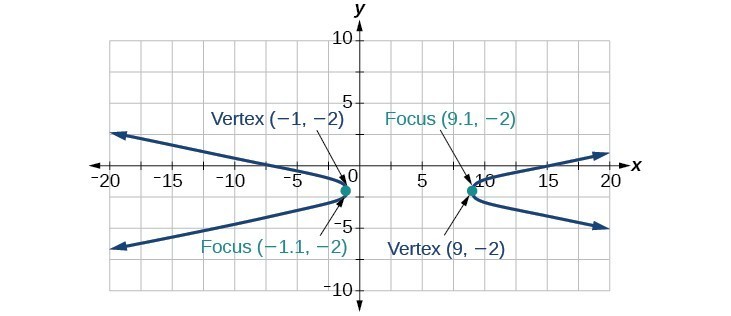 41.
41.
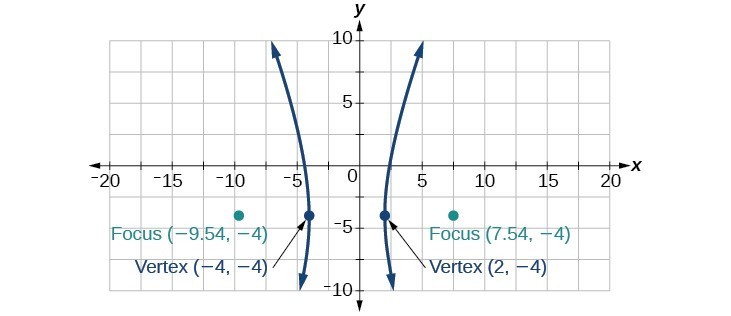 43.
43.
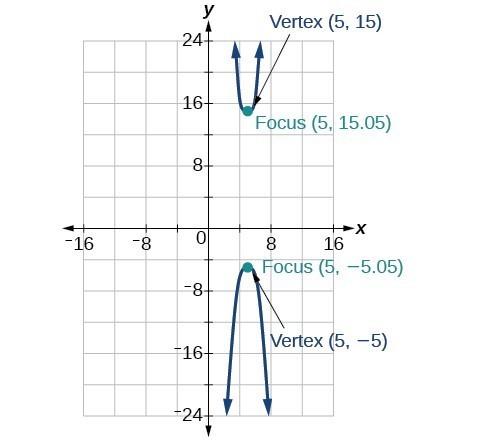 45.
47.
49.
51.
53.
55.
57.
45.
47.
49.
51.
53.
55.
57.
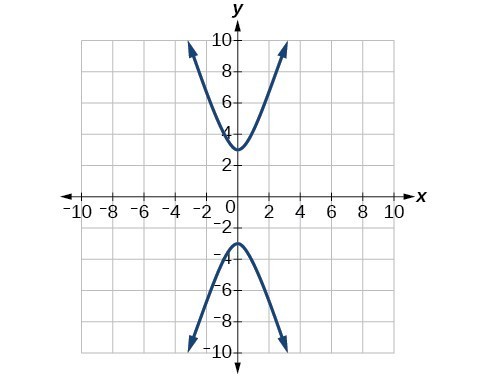 59.
59.
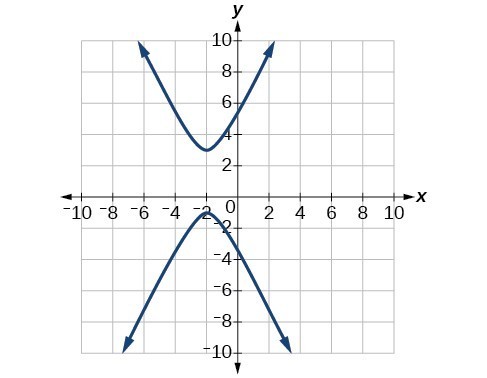 61.
61.
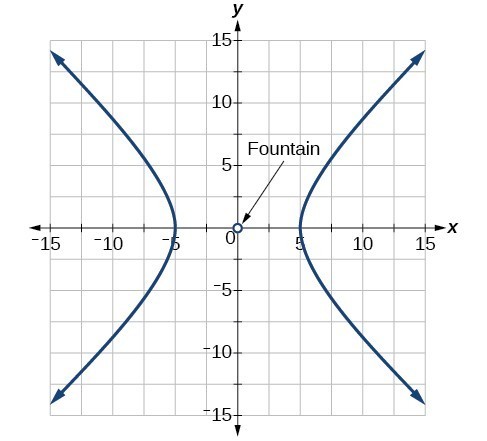 63.
63.
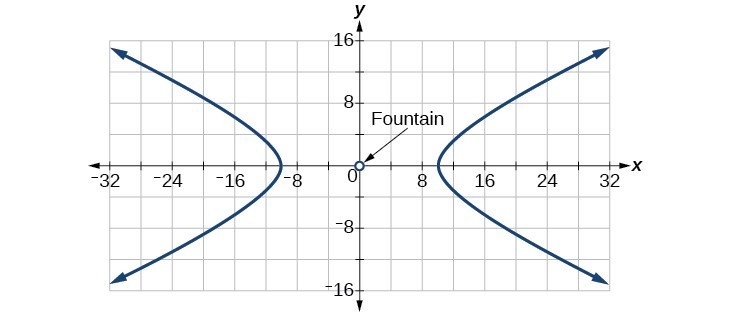 65.
65.
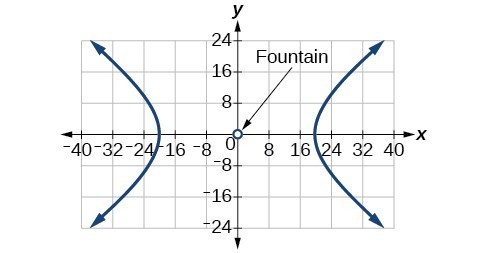 67.
69.
67.
69.