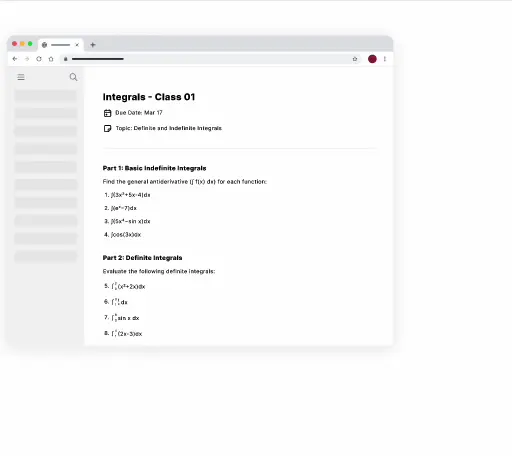
Section Exercises
1. If the terms of a polynomial do not have a GCF, does that mean it is not factorable? Explain. 2. A polynomial is factorable, but it is not a perfect square trinomial or a difference of two squares. Can you factor the polynomial without finding the GCF? 3. How do you factor by grouping? For the following exercises, find the greatest common factor. 4. 5. 6. 7. 8. 9. For the following exercises, factor by grouping. 10. 11. 12. 13. 14. 15. For the following exercises, factor the polynomial. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. For the following exercises, factor the polynomials. 37. 38. 39. 40. 41. 42. 43. 44. 45. 46. 47. 48. 49. 50. For the following exercises, consider this scenario: Charlotte has appointed a chairperson to lead a city beautification project. The first act is to install statues and fountains in one of the city’s parks. The park is a rectangle with an area of m2, as shown in the figure below. The length and width of the park are perfect factors of the area. 51. Factor by grouping to find the length and width of the park.
52. A statue is to be placed in the center of the park. The area of the base of the statue is . Factor the area to find the lengths of the sides of the statue.
53. At the northwest corner of the park, the city is going to install a fountain. The area of the base of the fountain is . Factor the area to find the lengths of the sides of the fountain.
For the following exercise, consider the following scenario:
A school is installing a flagpole in the central plaza. The plaza is a square with side length 100 yd. as shown in the figure below. The flagpole will take up a square plot with area yd2.
51. Factor by grouping to find the length and width of the park.
52. A statue is to be placed in the center of the park. The area of the base of the statue is . Factor the area to find the lengths of the sides of the statue.
53. At the northwest corner of the park, the city is going to install a fountain. The area of the base of the fountain is . Factor the area to find the lengths of the sides of the fountain.
For the following exercise, consider the following scenario:
A school is installing a flagpole in the central plaza. The plaza is a square with side length 100 yd. as shown in the figure below. The flagpole will take up a square plot with area yd2.
 54. Find the length of the base of the flagpole by factoring.
For the following exercises, factor the polynomials completely.
55.
56.
57.
58.
59.
54. Find the length of the base of the flagpole by factoring.
For the following exercises, factor the polynomials completely.
55.
56.
57.
58.
59.